Quelle est l’origine de l’air que nous respirons, de l’eau dans nos mers et océans, d’où vient la lumière du jour, pourquoi existe-t-il un climat terrestre, pourquoi des aurores boréales, pourquoi… ? La réponse se trouve dans le ciel. Les étoiles sont un formidable fournisseur d’éléments chimiques et notre Soleil est source de vie. Depuis des temps immémoriaux, l’homme s’est préoccupé d’en savoir toujours davantage sur les astres, leur mouvement, leur dimension, leur composition... Ainsi est née l’astronomie, qui nous renseigne sur les astres célestes. Lesquels sont décrits par diverses caractéristiques, masse, diamètre, rotation, température, composition chimique, etc., auxquelles s’ajoutent la place de ce corps dans l’univers, son histoire, voire, dans le cas du Soleil, ses répercussions sur l’histoire de l’humanité.
Les encyclopédies donnent les dernières mesures de notre étoile ; leurs valeurs font consensus, car validées par l’Union Astronomique Internationale. Ainsi la résolution B3 votée lors de l’AG de l’IAU le 13 Août 2015 recommande des valeurs nominales à adopter pour le diamètre, la luminosité, la température et la masse du Soleil. Mais il existe d’autres paramètres utiles pour développer de l’astrophysique solaire, c’est-à-dire expliquer des phénomènes mal compris, comme celui de la cyclicité des taches, lesquelles reviennent et disparaissent à échelle de onze années environ.
Parmi ces paramètres, l’un d’eux est encore quasiment inconnu et porte un nom difficile à comprendre du premier coup, comme il en serait de la notion de volume, nettement plus accessible. Il s’agit des moments gravitationnels solaires, qui peuvent paraître, même aux yeux de spécialistes, des « étrangetés ». Essayons de démystifier. Un corps en rotation s’aplatit aux pôles. Plus généralement, il se déforme. La déformation va dépendre de deux conditions, la vitesse de rotation (plus le corps tourne vite, plus il s’aplatit) et la composition interne. Il est aisé de comprendre que si le corps est rigide, comme une bille sphérique toute en acier, sa déformation (et donc son aplatissement) sera très minime. Mais si le corps possède une composition hétérogène, par exemple un noyau dense, enveloppé d’une ou de plusieurs strates moins denses non réparties uniformément autour du noyau, la déformation générale en surface présentera des écarts plus ou moins importants par rapport à une sphère idéale. Pour faire simple, un corps non homogène depuis le centre jusqu’en surface, et tournant à des vitesses différentes de l’équateur aux pôles, y compris à l’intérieur, va prendre une forme externe complexe, très « cabossée ». Ce sont ces déformations de surface que mesurent les moments gravitationnels (voir Figure 1).
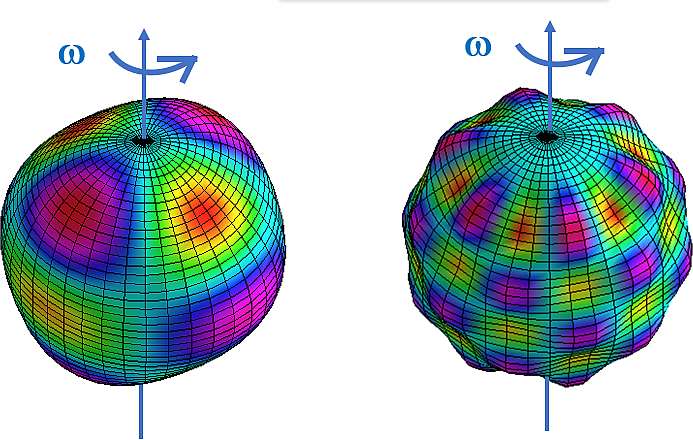
Figure 1 : Surface d’´équilibre d’un corps en rotation, sous l’effet de distributions de masse et de rotation non homogènes. Il en résulte des écarts à la sphéricité, mesurés par les coefficients liés directement aux « moments gravitationnels ». Le rendu de la surface « cabossée » se dévoile au fur et à mesure que l’on développe en moments gravitationnels d’ordre de plus élevés (n=1, 2, 4, 7…).
Plusieurs tentatives ont été faites au cours des siècles passés pour calculer ces moments gravitationnels, que ce soit dans le cas de la terre (et oui, la terre n'est pas sphérique !), des planètes rocheuses ou des étoiles. Dans le cas de planètes rocheuses, la théorie, complétée par des résultats déduits de satellites dédiés, est devenue très robuste et permet d’obtenir des valeurs des moments gravitationnels extrêmement précises. Par exemple pour Mars, J2 vaut 0.001860718 (à partir d’un modèle comportant 73 termes (!) décrit par Yuan en 2002). Pour Cérès, une petite planète de notre système solaire, J2 vaut 0.03240, J4 -0, 00237 et J6 0.00237, permettant en retour de se donner une idée de la composition interne de l’astre, comme l’a décrit Rambeaux en 2015.
Pour décrire ces moments gravitationnels, les physiciens des siècles passés se sont régalés à chercher des formes analytiques, c’est-à-dire des formules plus ou moins complexes élaborées à partir de la connaissance des propriétés physiques du corps (masse, densité…) et de sa vitesse de rotation, permettant in fine d’effectuer le calcul. Cela est possible pour un corps de densité uniforme en rotation constante. Newton, en 1867, est le premier à établir une formule simple mais approchée, reprise sous une forme toujours valable de nos jours par Huygens en 1690. En 1743, Clairaut, un physicien français s’attaque de nouveau au problème et en donne une formulation élégante, toujours dans le cas d’un corps tournant à vitesse constante, mais de densité variable ρ(r). L’idée à l’époque était de trouver la meilleure figure d’équilibre de la surface externe de la Terre, d’autant que l’on pouvait confronter la théorie aux observations. Clairaut sera suivi par beaucoup d’autres, tels que Bruns en 1878, qui introduisit le concept de « Figure d’un corps en rotation », puis Radeau en 1885, Wavre en 1932, Molodensky en 1945 ou Moritz en 1990, pour n’en citer que quelques-uns, et qui tous, raffinèrent les modèles.
Chandrasekhar (astronome américain d’origine indienne, nobelisé en 1983) s’intéressa dès 1933 au cas des étoiles, pour lesquelles il développera une théorie très complète, mais toujours dans le cas d’une rotation uniforme. Le problème est plus difficile, car il s’agit d’un corps fluide. La théorie a été ensuite considérablement améliorée notamment par Maeder, en 1999, qui en donna une formulation plus générale. La physique sous-jacente est très complexe car la rotation influe sur l’évolution stellaire et des transports d’éléments chimiques internes à l’étoile peuvent avoir lieu. Alors comment tous ces effets façonnent-ils la surface observée ? Qu’est-elle dans le cas du Soleil, astre non homogène du centre vers la surface (la quasi-totalité de la masse est concentrée dans une couche occupant le premier quart interne), en rotation non uniforme, à la fois également du centre vers la surface, mais aussi de l’équateur aux pôles ?
Mais pourquoi les déformations de surface sont-elles appelées de ce terme un peu barbare, moments gravitationnels ? Pour comprendre, dans le cas d’un astre en rotation, un petit volume de masse (m) à sa surface, où à l’intérieur, subit deux forces. L’une a pour origine l’attraction gravitationnelle de cet astre (comme si la totalité de sa masse était concentrée en son centre) avec les autres corps proches ou très massifs, la lune, le soleil, les planètes… et l’autre, une force dont l’origine est sa rotation propre. La somme de ces deux forces est appelée “pesanteur” (en anglais, pesanteur se traduit par « gravity »). Moment parce qu’en physique, le moment d’une force traduit la faculté pour cette force de faire tourner le système. On parle donc de moment gravitationnel pour exprimer le fait que les « cabossages » successifs sont dues à la gravitation et à la rotation. Le moment gravitationnel d’ordre 1, dit J1, traduira une figure finale en forme de « poire », tandis que celui d’ordre 2, dit J2, traduit une forme aplatie, comme un ballon de rugby, et au fur et à mesure que les ordres s’élèvent, 3, 4… la figure externe est de plus en plus complexe. Il faut bien voir toutefois qu’il s’agit là d’une représentation pragmatique, la réalité physique étant plus complexe. Cependant cette série de paramètres que sont les moments gravitationnels vont un par un nous renseigner sur la figure d’équilibre de la surface externe de l’enveloppe du corps étudié.
Pour le soleil, la situation est plus complexe. Pendant très longtemps, les Jn et J2 en premier n'ont guère suscités d'intérêt en raison de deux faits significatifs : d'une part, leurs ordres de grandeur sont très faibles. D'autre part, ils ne peuvent pas être mesurés directement, des modèles sont requis, et donc les valeurs seront dépendantes du modèle adopté. Sur le premier point, s’appuyant sur un très grand nombre de résultats, Pireaux & Rozelot en 2003, ont pu attribuer à J2 une valeur d’environ 0.2 partie pour un million [soit (2,0 ± 0,4) × 10-7], maintenant communément admise. Sur le second point, plusieurs observations indirectes ont été proposées, les résultats confortant la valeur indiquée ci-dessus. Comme J2 est directement relié à l’aplatissement, il en résulte que le diamètre polaire du Soleil est plus court d’environ 12 km que le diamètre équatorial, pour un diamètre moyen de quelques 1 391 000 km (soit 8.6 parties pour un million !) Les moments gravitationnels d’ordre plus élevés sont encore plus faibles et sont, pour l’instant du moins, pas pris en compte (et leur ordre de grandeur mal défini).
On peut se demander l’intérêt de courir derrière une valeur qui avoisine zéro… Au moins pour trois raisons. La première est de donner les valeurs les plus précises possibles des paramètres qui caractérise un astre, dont le Soleil. C’est ce qu’on appelle l’astrométrie, une science en pleine vigueur au début du siècle passé, toujours d’actualité quand il s’agit de décrire finement les propriétés d’un corps céleste. Par exemple, l’aplatissement des étoiles. Les mesures sont encore très difficiles parce qu’à la limite de détection des instruments. Cependant, les cartes d’identité du Soleil, des planètes, des étoiles, doivent être fournies et satisfaisantes.
La seconde tient au fait que dans certaines formules de mécanique céleste, il faut tenir compte des moments gravitationnels. Dans notre système solaire, les orbites des planètes partagent un plan commun à quelques degrés près. Cette coplanarité a été héritée d'un disque protoplanétaire (déjà découvert par Laplace en 1796) et a été conservée tout au long des 4,5 milliards d'années de l'histoire de notre système solaire… Le calcul précis de l’inclinaison des orbites tient compte des moments gravitationnels. De même pour les systèmes planétaires extrasolaires qui se forment également dans des disques minces (mais on ignore quelle proportion de ces systèmes conserve leur coplanarité primordiale tout au long de leur vie). A l'exception de cas particuliers limités, les inclinaisons mutuelles sont généralement difficiles à mesurer. Dans les systèmes déjà connus pour posséder plusieurs planètes en transit, les inclinaisons ont tendance à être faibles, de l'ordre de ∼ 1 - 2◦, augmentant quand elles sont au plus près de l'étoile. Un mécanisme de désalignement a été proposé par Spalding en 2020, qui met en œuvre le moment gravitationnel de l’étoile hôte en rotation rapide.
La troisième raison fait appel à la détermination précise des éphémérides, c’est-à-dire la prévision de la position des astres dans le ciel au cours du temps. Des almanachs célestes et nautiques sont ainsi élaborés par trois instituts indépendants, l’un en Russie (EPM à Saint-Pétersbourg), un autre aux USA (JPL, à Pasadena) et le dernier à Paris (IMCCE). Ces éphémérides sont calculées à partir d’observations de plus en plus précises (Laser-lune, observations radar de planètes, suivi de satellites, interférométrie à très longue base...) et qui permettent d’obtenir, par exemple dans le cas de notre système solaire, des positions de planètes à quelques mètres près ! La détermination de ces orbites fait appel aux moments gravitationnels, qui peuvent être déduits des mesures spatiales par un procédé d’ajustement successif des données aux résultats. Procédé un peu compliqué mais qui donne de bons résultats, par exemple dans le cas de la sonde spatiale Messenger, en orbite autour de Mercure, la méthode donne pour le Soleil, J2 0.2246 partie pour un million [J2 = (2.246 ± 0.022)× 10−7 ]. La grande précision obtenue permet de remonter aux paramètres de la relativité générale (RG) et d’en prouver l’universalité (autrement dit, les théories alternatives à la RG sont peu probables).
Cet article est novateur à plus d’un titre. En premier lieu, il réaffirme la valeur nominale du J2 solaire, qui serait bien de 0.207 parties par million [J2 = (2.07 ± 0.03) × 10−7]. De plus, il met en évidence une variabilité temporelle : la modulation d’amplitude varie sur une échelle de temps de 90 ans environ. Cela permet d’expliquer que les valeurs trouvées à différentes époques, à partir d’observations, peuvent différer quelque peu. De plus, les auteurs montrent pour la première fois que le moment gravitationnel solaire d’ordre 1 (soit J2) est corrélé négativement avec le cycle solaire lorsque celui est en période de maximum, et vice versa (corrélation plus forte avec le cycle en période de minimum). Ce mécanisme pourrait prendre place dans une couche de sous-surface solaire (appelée leptocline -du grec leptos, fin) mise en évidence par l’auteur dès 2001 et validée par deux auteurs américains, Kitashvili et Kosovichev dans un modèle à 3 dimensions en 2022. Un tel résultat original pourra être ultérieurement incorporé dans les théories visant à mieux comprendre comment la machine solaire fonctionne avec le temps. Il s’agit donc d’une belle avancée dans le domaine de la physique solaire.
Référence
Exploring the Temporal Variation of the Solar Quadrupole Moment J2, Astrophysical Journal (ApJ - AAS41872).
Contacts
Saliha Eren, The Arctic University of Norway, Department of Physics and Technology, Postboks, saliha.eren@uit.no
Jean-Pierre Rozelot (OCA-retired), jean-pierre.rozelot@grenoble-inp.org
