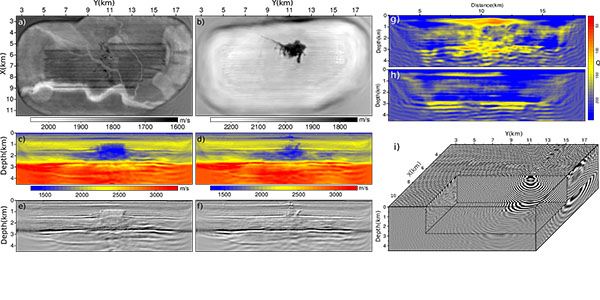
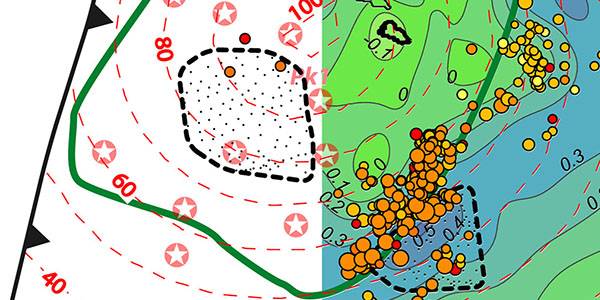
![]() En 2011, les études expérimentales et géologiques dans le cadre du consortium pétrolier GeoFracNet ont mis en évidence pour la première fois que les fractures les plus courantes sur Terre, les diaclases, se forment à partir des bandes dilatantes pures de la localisation de la déformation (1,2,3). Le mécanisme physique de ce phénomène n’était cependant pas encore compris.
En 2011, les études expérimentales et géologiques dans le cadre du consortium pétrolier GeoFracNet ont mis en évidence pour la première fois que les fractures les plus courantes sur Terre, les diaclases, se forment à partir des bandes dilatantes pures de la localisation de la déformation (1,2,3). Le mécanisme physique de ce phénomène n’était cependant pas encore compris.
Les travaux théoriques et numériques d’Alexandre Chemenda, enseignant-chercheur UCA à Géoazur (UNS, CNRS, OCA, IRD) ont permis d’élucider et de reproduire, dans des modèles numériques, chaque étape du processus de cette fracturation. Les résultats de ces travaux viennent de paraitre dans Journal of Geophysical Research: Solid Earth du mois de juillet 2019.
Les diaclases forment souvent des réseaux spectaculaires très réguliers (Fig. 1) et ont une importance pratique capitale dans la production des fluides économiques tels que l’eau, le gaz, ou le pétrole.

Fig. 1. Réseau de diaclases dans un banc de grés (Eaglehawk Neck, Tasmania) (5).
C’est notamment pour cette raison que les diaclases sont des objets d’études intensives depuis plus d’un siècle. Selon la vision classique basée sur « Linear Elastic Fracture Mechanics » (LEFM), ces fractures se formeraient dans une roche très fragile à partir de défauts/hétérogénéités préexistants, concentrateurs de contraintes. Or, la régularité (i.e., parallélisme) des diaclases naturelles suggère, au contraire, qu’elles se forment dans un matériau et dans un champ de contraintes très homogènes.
Malheureusement, on ne peut pas observer, étudier et donc connaitre les conditions et le déroulement de la formation des diaclases naturelles. Il était cependant possible d’étudier ce processus en laboratoire dans des expériences où les diaclases et leurs réseaux réguliers ont été obtenus/reproduits dans un matériau homogène analogue des roches GRAM (1, 3) (Fig. 2).

Fig. 2. Réseau parallèle de diaclases généré dans une couche d’un matériau analogue des roches (GRAM – Granular Rock Analoque Material)
insérée entre deux couches de caoutchouc sous l’extension dans une direction σ_3 et la compression dans les deux autres directions comme représenté sur Fig. 3(3).
Ces expériences ont permis de révéler que la formation d’une fracture au stricto sensu (ayant un espace ouvert entre ses bords) est précédée par la localisation de la déformation inélastique ou endommagement dans une bande orientée normalement à la contrainte minimale σ_3 et dont l’épaisseur ne dépasse pas plusieurs tailles de grains. La porosité à l’intérieur de cette bande est augmentée (le matériau est dilaté) et la résistance est réduite.
La fracture résulte de l’évolution de cette bande de dilatance qui était difficile à déterminer expérimentalement. Elle est donc restée non comprise. D’autre part, d’après le paradigme dominant (LEFM), la rupture totale du matériau est supposée suivre directement la déformation élastique et se produire dans une zone très petite (dans un « point ») au bout de la fissure préexistante. Ainsi, aucune formation de bande d’endommagement n’était envisageable. Cette contradiction entre la vision classique et les résultats expérimentaux devait être levée en proposant une explication physique crédible de ces résultats.
Il a fallu des années d’études expérimentales, de développements théoriques et numériques pour mener à bout une nouvelle approche sur la formation des diaclases. Dans l’article qui vient de paraitre (4), Alexandre Chemenda présente les résultats expérimentaux qui montrent que la fracturation des géomatériaux dits très fragiles est précédée et accompagnée d’une déformation inélastique (endommagement) non-négligeable qui doit donc être prise en compte dans des modèles théoriques. Il s’est avéré que cette déformation est nécessaire à la structuration/formation des réseaux de diaclases réguliers.
Un nouveau modèle constitutif (loi de compartiment) a été formulé : il décrit l’endommagement cisaillant et « tensile » en couplant l’évolution de la résistance en traction σ_t et en compression avec la déformation. Les modèles numériques utilisant cette loi et correspondant à trois couches sédimentaires ont été déformés sous l’extension horizontale et la pression lithostatique (profondeur) constante (Fig. 3).
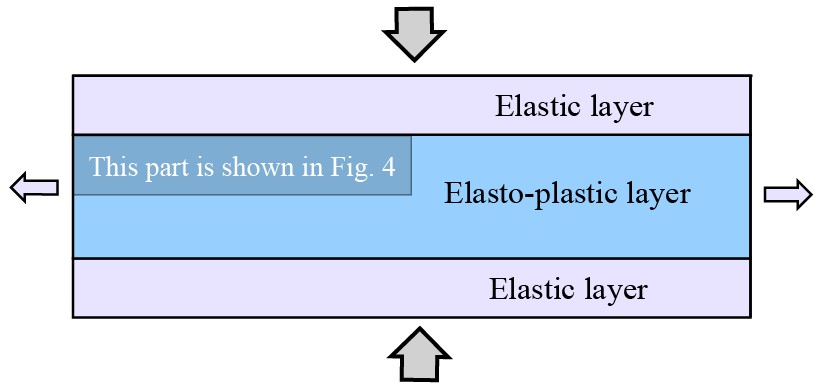
Fig. 3. Schéma des modèles numériques (ainsi que des modèles expérimentaux GRAM sur la Fig. 2) et les forces appliquées.
La fracturation a d’abord commencé par un endommagement diffusé puis localisé au sein d’un réseau dense de bandes de dilatance émanant des interfaces entre les couches (Fig. 4a, 2ème colonne). Certaines de ces bandes ont traversé la couche entière et d’autres ont été abandonnées à différents stades de leur évolution (Fig. 4, 2ème colonne). L’endommagement conduit à la rupture progressive du matériau à l’intérieur des bandes, ce qui se traduit par une réduction de la résistance en traction (Fig. 4, 1ère colonne).
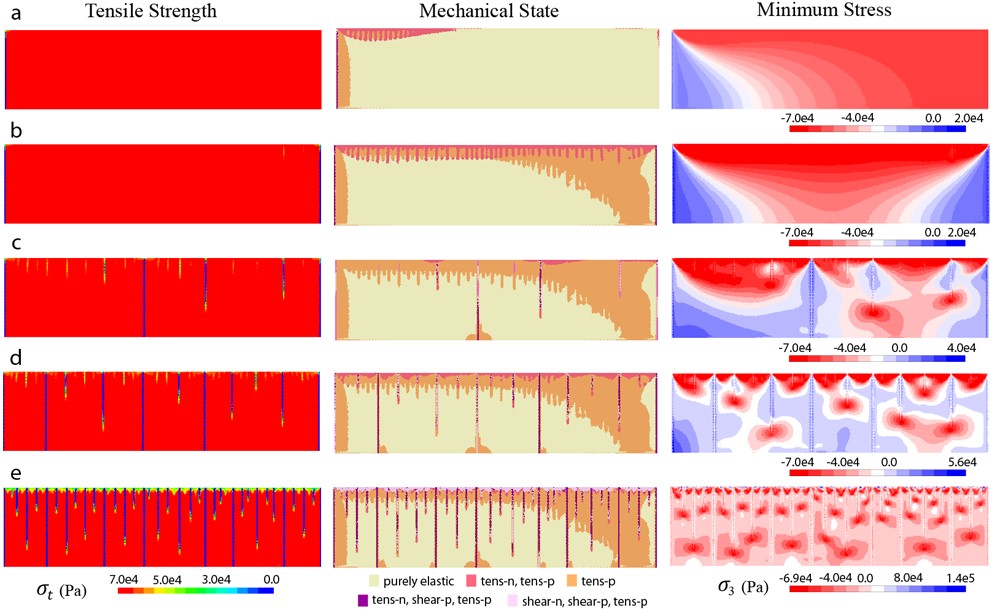
Fig. 4. Cinq stades (de a à e) de l’évolution de la résistance en traction σ_t (1ère colonne), de l’état mécanique, élastique ou élasto-plastique et de l’évolution des mécanismes d’endommagement (2ème colonne),
ainsi que de la contrainte minimale σ_3 (3ème colonne). Un quart de la couche centrale montrée sur la Fig. 3 est présentée ; la fracturation des trois autres quarts peut être reconstituée en tenant compte de la symétrie du problème.
Les différentes couleurs dans la 2ème colonne correspondent aux différents mécanismes d’endommagement et leurs successions décrits dans le détail dans l’article original (4).
Dans cette note, il est important de seulement montrer les bandes verticales de la localisation de l’endommagement, les bandes de dilatance, et leur croissance.
Aux stades a et b, les bandes sont déjà initiées ((Fig. 4, 2ème colonne), mais la réduction de σ_t est encore très petite et pratiquement invisible. Des fractures sont initiées à l’intérieur des bandes lorsque le matériau est complètement cassé et σ_t devient zéro. Ceci perturbe fortement le champ des contraintes qui évolue avec le réseau des bandes/fractures (Fig. 4, 3ème colonne). La longueur et l’épaisseur des bandes sont proportionnelles à la ductilité du matériau qui varie selon les modèles. Comme indiqué ci-dessus, l’évolution de certaines bandes s’arrête à différents stades et celles-ci ne deviennent jamais des fractures. Ce sont ces bandes appartenant à un réseau orthogonal de diaclases qui ont été mises en évidence par J.-P. Petit dans un affleurement de dolomicrite3. Toutes les fractures émanant des limites horizontales de la couche ne la traversent pas complètement (Fig. 4e). C’est aussi le cas dans les modèles expérimentaux (Fig. 2) et dans des exemples naturels.
Le travail présenté ici recoupe différentes approches : expérimentale, géologique, théorique et numérique et ouvre une voie pour des applications pratiques par modélisation de la fracturation des structures 3D complexes dans des réservoirs géologiques.
Publications
1. Chemenda, A. I., Nguyen, Si-H., Petit J.P., Ambre, J. (2011a), Mode I cracking versus dilatancy banding: Experimental constraints on the mechanisms of extension fracturing, Journal of Geophysical Research: Solid Earth, 116, B04401, doi:10.1029/2010JB008104.
2. Chemenda, A. I., Nguyen, Si-H., Petit J.P. Ambre, J. (2011b), Experimental evidences of transition from mode I cracking to dilatancy banding, Comptes Rendus, Mécanique, 339, 219-225, doi:10.1016/j.crme.2011.01.002.
3. Jorand, C., Chemenda, A. I., Petit, J-P. (2012), Formation of parallel joint sets and shear band fracture networks in physical models, Tectonophys., 581, 84-92, doi: 10.1016/j.tecto.2011.11.021.
4. Chemenda, A. I. (2019, in press). Origin of regular networks of joints: Experimental constraints, theoretical background, and numerical modeling. Journal of Geophysical Research: Solid Earth, 124. https://doi.org/10.1029/2019JB017454.
5. Référence CNRS-INSU http://www.insu.cnrs.fr/en/terre-solide/lithosphere-continentale/les-fractures-les-plus-courantes-de-l-ecorce-terrestre-enfin-m;
Référence Géoazur https://geoazur.oca.eu/fr/actu-scient-geoazur/1297-les-fractures-les-plus-courantes-de-l-ecorce-terrestre-enfin-modelisees
Contact
Alexandre Chemenda, Géoazur UCA (UNS- CNRS-IRD/OCA)
chem@geoazur.unice.fr
04 92 94 26 61
Information parue dans les actualités UCA